Plate bending
Description
A thin rectangular plate, simply supported along all four edges, subject to a uniformly distributed area load.
Geometry
Dimensions: 10 x 16 [m]; Thickness: 0.2 [m]
Modulus of Elasticity: 1,000,000; Poisson ratio: 0.3
Elements: 10 x 16 grid rectangular elements.
Supports: Pinned (restrained against rotation parallel to edge).
Loads
Uniform pressure: -1.0 [T/m^2] in the X3 direction on all elements.
Reference
Timoshenko and Woinowsky-Kreiger, Theory of Plates and Shells, 2nd Edition. (Chapter 5, table 6),
McGraw-Hill Book Company
Comparison of Results
| Element | Node | Result type | Result | Deviation | |
| Theoretical | STRAP | ||||
| – | 166 | Deflection | 0.11341 | 0.11317 | 0.21% |
| 86 | 166 | Mx | 8.62 | 8.652 | 0.37% |
| 86 | 166 | My | 4.92 | 4.936 | 0.32% |
Concrete design moments
Description
The plate bending model of example 3.10 is used to verify the calculation of the concrete design moments (Wood & Armer).
The Wood & Armer equations are listed in the STRAP User’s Manual. Note that these equations are based on the standard engineering sign convention (sagging moment = positive), while the STRAP sign convention gives opposite results (sagging moment = negative). For clarity, the calculations in this example use the standard engineering sign convention.
Geometry / Loads
Refer to the previous plate bending example.
Reference
R.H. Wood, “The Reinforcement of Slabs in Accordance with a Pre-determined Field of Moments”.
“Concrete” magazine – February 1968
STRAP Results
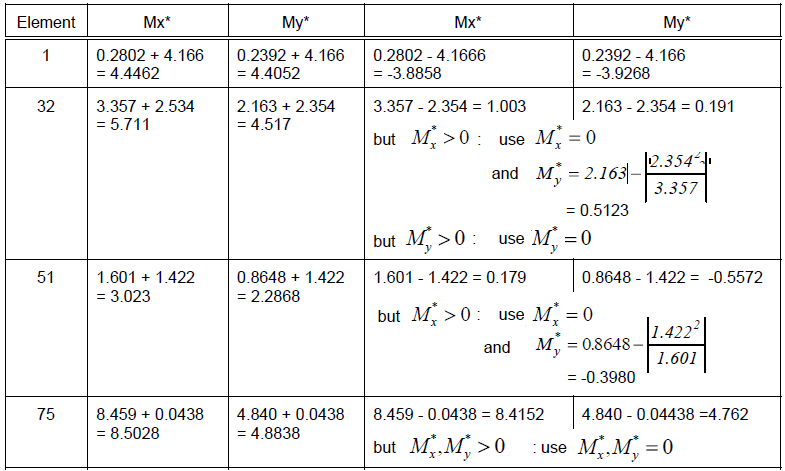
| Element | Element results | Wood & Armer moments | |||||
| Bottom | Top | ||||||
| Mx | My | Mxy | Mx* | My* | Mx* | My* | |
| 1 | 0.2802 | 0.2392 | 4.166 | 4.446 | 4.405 | -3.885 | -3.926 |
| 32 | 3.357 | 2.163 | 2.354 | 5.711 | 4.517 | 0.0 | 0.0 |
| 51 | 1.601 | 0.8648 | 1.422 | 3.023 | 2.286 | 0.0 | -0.3975 |
| 75 | 8.459 | 4.840 | 0.0438 | 8.503 | 4.884 | 0.0 | 0.0 |
Calculation of Results
The Wood & Armer moments were verified by hand calculation and are summarized in the following table. The results are identical.